Problem Description

The Order Batching and Sequencing Problem is an optimization problem that involves the process of collecting orders in a warehouse. Each order received in a warehouse, composed by a list of items to be collected, is grouped with other orders in a certain batch of a maximum fixed capacity. A routing algorithm is applied to each batch to know the time that a worker spends collecting all the items.

In this variant, each order has a certain due date, i.e., each order must be collected before an specific time. If an order is not collected before its due date, it is said to have a tardiness.

The problem consists in grouping orders into batches, sequencing and routing them, in such a way that the total tardiness is minimized.

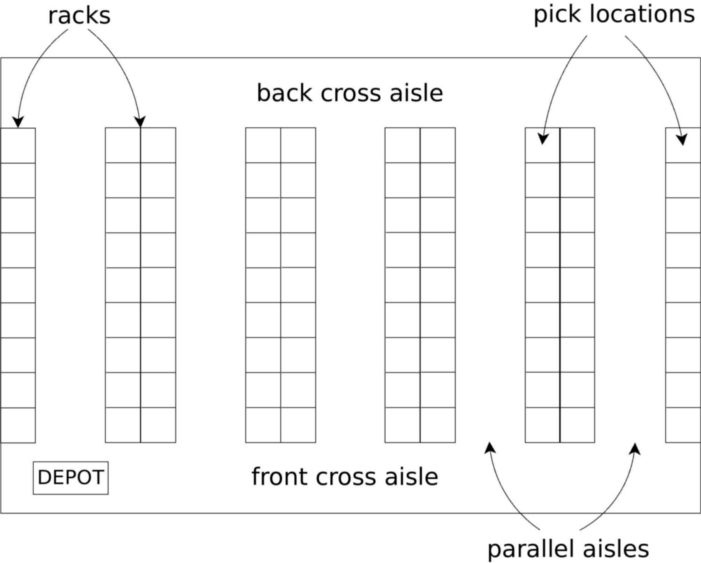
This problem is divided into three different problems: the grouping of orders into batches (batching), the order the batches are collected from the warehouse (sequencing) and the path that a worker must follow to collect the orders (routing).

State of the Art Methods

Du and Leung (1990) have shown that the problem of minimizing the total tardiness for a set of independent jobs on a single machine is N P-hard. This problem can be interpreted as a special case of the OBSP, in which the capacity of the picking device is equal to only one customer order. As Henn et al. (2010) states, we can conclude that the OBSP is also N P-hard. Therefore, the problem have been heuristically approached in the last few years.

The OBSP has been recently studied in Henn and Schmid (2013), by using a modified version of the Iterated Local Search (ILS) and the Attribute-Based Hill Climbing (ABHC). These two methods were originally introduced in Henn et al. (2010) and Henn and Wäscher (2012), respectively, to solve a variant of the OBSP. The authors compared these two algorithms by considering the relative improvement with respect to the EDD method. They also introduce a huge set of instances, which covers different parameters such as the capacity of the picking cart, the number of orders used, or the Modified Traffic Congestion Rate (MTCR) (Elsayed and Lee, 1996). This last parameter is relevant for the OBSP since it determines the tightness of the problem regarding the due dates. The larger the MTCR, the closer the due dates, and vice versa.

Hossein et al. (2013) proposed a hybrid approach based on combining different techniques. First of all, the algorithm starts by calculating associations between orders within each batch with a Weighted Association Rule Mining procedure (MINWAL) (see Chen and Wu, 2005). With this procedure, orders with similar due dates and similar items have larger probabilities of being in the same batch. Next, a Binary Integer Clustering model is applied to construct batches maximizing the associations among orders within each batch. Afterward, a Genetic Algorithm identifies the most suitable travel path. Finally, the method applies another Genetic Algorithm for sequencing the constructed batches to minimize tardiness.

The last attempt to address this problem has been driven by Chen et al. (2015) which present both, an exact and an approximate approaches. The first one is based on a Non-linear Integer Optimization model. They proposed a heuristic method based on a hybridization between a Genetic Algorithm and an Ant Colony Optimization (ACO) procedure.

Instances

We have experimented with one set of instances, totalizing 96 instances:

• Henn and Wäscher, 2012: This collection of instances consists of a rectangular warehouse with 10 aisles and 90 storage locations each. The depot is always located at the bottom left corner. The item distribution is both (i) ABC distribution and (ii) random distribution. Customer orders varies from 40 to 100 in steps of 20 and the capacity of the picker ranges between 30 and 75 in steps of 15.

The comparison has been made against one subsets of instances. These instances are a subset of Henn and Wäscher, 2012 containing 96 instances. These instances were used to compare our algorithm against the state-of-the-art algorithms.

You can download Order Batching and Sequencing Problem instances here.

Computational Experience

All the algorithms were implemented in Java SE 7 and the experiments were conducted on an AMD Phenom II X6 1050T with 2.8 GHz and 4 GB of RAM with Ubuntu 14.04 64 bit OS. We have considered the instances described above. The individual results for each instance can be downloaded here in Excel format.

Results for the comparison against ILS combined with S-Shape and ILS combined with Largest Gap.