Problem Description

The Online Order Batching Problem (OOBP) is a variant of the well-known Order Batching Problem (OBP) which consist of grouping the orders arrived to a warehouse (each order is composed by a list of items) in a set of batches in such a way that the time needed to collect all the orders is minimized. Additionally, each batch has to be collected by a single picker without exceeding a capacity limit.In the online variant of the OBP, the arrival of orders is dynamic. In this way, the system only knows a small group of orders to collect in the moment when the picking starts, since orders arrive to the warehouse throught the time. To deal with this problem, researchers study the orders received in the warehouse during a particular period of time.

We center our attention in rectangular warehouses with different number of parallel aisles and two cross aisles (one at the front and one at the back of the warehouse) with a depot placed at the front cross aisle (either in the left most corner or in the center of the aisle). Next, we depict the considered warehouse in a figure:

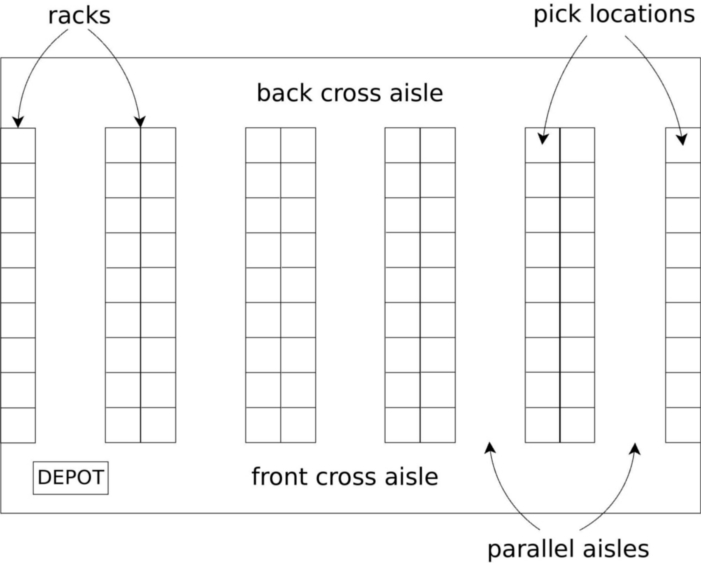
The OOBP consist of handling with four different optimization problems: i) grouping of orders into batches; ii) sequencing the order in which batches are collected; iii) finding a route to collect the orders in the selected batch; and iv) determining the time that the picker waits until he/she starts the picking (i.e., the time window).

Next, we depict the time line of the life of an order, and the time line of the life of a batch through the time, in the context of the OOBP:

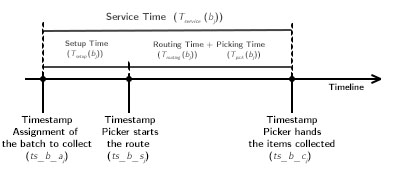
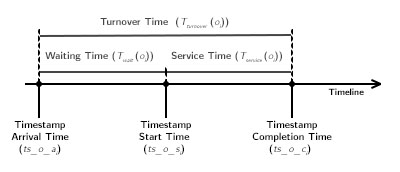
State of the Art Methods

This problem has been proved to be NP-hard for general instances. Nonetheless, it is solvable in polynomial time if each batch does not contain more than two orders. Unfortunately, real warehouse instances does not usually fall into this category.

The variant of the OOBP compared in this paper was first tackled by Henn in 2012. They proposed a heuristic algorithm based on Iterated Local Search (ILS) to minimize the maximum completion time of the orders from the customers, which arrive to the system within a certain time period. In this paper, the authors also reported two other objective functions (the maximum and the average time that an order remains in the system). The ILS method was compared with a classical FCFS algorithm and with a Clarke and Wright method.

The variant of the problem previously presented was also tackled later by Perez-Rodriguez et. al. in 2015. The authors proposed a variant of the well-known Estimation of Distribution Algorithm (EDA) to tackle the problem. The authors reported the average distance traversed by the picker as objective function. However, the proposed EDA was not able to improve previous results.

In 2011, Rubrico et al. tackled a related problem, the Online Rescheduling Problem with multiple pickers. However, this variant of the problem, despite of its close relation with the OOBP, is not comparable to the two previous approaches since they consider multiple pickers and introduces a rescheduling procedure. The authors proposed two heuristic methods based on the Steepest Descent Insertion strategy, and on the Multistage Rescheduling strategy. In this case, the objective function tackled is to minimize the maximum total travel distance traversed by each picker.

Other different variant of the problem was tackled by Zhang et. al., 2016. In this paper the OOBP was integrated with the scheduling of the delivery, trying to minimize the service time of an order.

Instances

We publish in this site two sets of instances used in the context of the OOBP, totalizing 144 instances: the first one is a subset of Albareda-Sambola et al., 2009 and contains 80 instances. The second one is a subset of Henn and Wäscher, 2012 containing 64 instances. These 144 instances were used to compare our algorithm (GRASP+VND) against the ILS (Henn, 2012) method in the state of the art.

Sets of instances

• Henn and Wäscher, 2012: This collection of instances consists of a rectangular warehouse with 10 aisles and 90 storage locations each. The depot is always located at the bottom left corner. The item distribution is both (i) ABC distribution and (ii) random distribution. Customer orders varies from 40 to 100 in steps of 20 and the capacity of the picker ranges between 30 and 75 in steps of 15.
• Albareda-Sambola et al., 2009: This set consists of four different rectangular warehouses with the depot located either at the bottom left corner or at the bottom center of the warehouse. The item distribution is also both (i) ABC distribution and (ii) random distribution. The number of orders varies from 100 to 250 in steps of 50 and the capacity of the picker depends on the warehouse.

Instances are ready to be executed over a time horizon of 4 hours. In order to ease future ocmparisons, the moment in the time when each order (for each instance) arrives to the warehouse is provided (see the readme.txt file of the instances). Instances can be downloaded here.