Problem Description

The MinMax Order Batching Problem consist of grouping the orders (composed by a list of items) received in a warehouse in a set of batches in such a way that the maximum time needed to collect each batch is minimized. Each batch have to be collected by a single picker without exceeding a capacity limit.

We center our attention in rectangular warehouses with parallel aisles and two cross aisles (one at the front and one at the back of the warehouse), with a depot at the front cross aisle (or, as in the next figure, at the bottom, either left or centered):

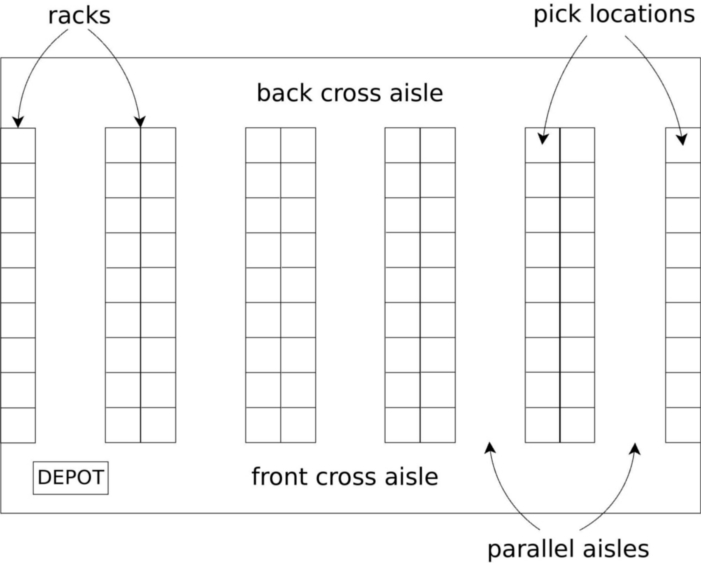
This problem is divided into two different problems: the grouping of orders into batches and the routing to collect them.

State of the Art Methods

Gademann et al. (2001) introduced the Min-Max Order Batching Problem (Min-Max OBP) variant, which considers that a number of batches is collected simultaneously by a group of pickers. It is usually denominated as wave picking operation. This problem is related to the Order Batching Problem.

In the context of warehousing, these operations are applied when the set of orders to retrieve is large and, thus, the collecting time is important. Min-Max OBP assumes that each picker collects the items of one batch and all the pickers start their routes at the same time.

The objective function in this variant is to minimize the maximum retrieving time of any of the batches. This variant was exactly solved by Gademann et al. (2001) with a Branch and Bound algorithm with four different lower bounds and a straightforward heuristic for the upper bound.

Instances

We have experimented with two sets of instances, totalizing 144 instances:

• Henn and Wäscher, 2012: This collection of instances consists of a rectangular warehouse with 10 aisles and 90 storage locations each. The depot is always located at the bottom left corner. The item distribution is both (i) ABC distribution and (ii) random distribution. Customer orders varies from 40 to 100 in steps of 20 and the capacity of the picker ranges between 30 and 75 in steps of 15.
• Albareda-Sambola et al., 2009: This set consists of four different rectangular warehouses with the depot located either at the bottom left corner or at the bottom center of the warehouse. The item distribution is also both (i) ABC distribution and (ii) random distribution. The number of orders varies from 50 to 250 in steps of 50 and the capacity of the picker depends on the warehouse.

The comparison has been made against two subsets of instances. The first one is a subset of Albareda-Sambola et al., 2009 and contains 80 instances. The second one is a subset of Henn and Wäscher, 2012 containing 64 instances. These 144 instances were used to compare our algorithm against ABHC and VND state-of-the-art algorithms.

The total number of instances is 144 and you can download Min-Max Order Batching Problem instances here.

Computational Experience

All the algorithms were implemented in Java SE 7 and the experiments were conducted on an Intel Core i7 2.4 GHz and 4 GB RAM. We have considered the instances described above. The individual results for each instance can be downloaded here in Excel format.

Results for the comparison against Gademann et al.