Solver Description

EvoPR applies the path relinking (PR) methodology to the problem of finding a global optimum of a multimodal function. In particular, we target large-scale problems with box constraints, and compare two variants of PR methodology: the static and the evolutionary path relinking (EvoPR). Both are based on the strategy of creating trajectories of moves passing through high-quality solutions in order to incorporate their attributes to the explored solutions. Computational comparisons are performed on a test-bed of 19 global optimization functions previously reported with dimensions ranging from 50 to 1,000, totalizing 95 instances. Our results show that the EvoPR procedure is competitive with the state-of-the-art methods in terms of the average optimality gap achieved. Statistical analysis is applied to draw significant conclusions.

We assume that a problem instance consists of finding a set of values for x = (x₁, x₂, ..., x_n) - where x_i is a real number - in order to minimize a multimodal function, given that l_i <= x_i <= u_i.

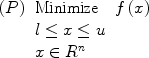
Functions used for Testing

We have used 19 multimodal functions to test our procedure (see the special issue page for more details). Solutions to these problems are naturally represented as real-number vectors:

1. 6 Functions: F1-F6 of the CEC'2008 test suite
2. 5 Shifted Functions: Schwefel’s Problem 2.22 (F7), Schwefel’s Problem 1.2 (F8), Extended f10 (F9), Bohachevsky (F10), and Schaffer (F11)
3. 8 Hybrid Composition Functions (F12-F19*): They are non-separable functions built by combining two functions belonging to the set of functions F1-F11

A document with a complete description of these functions can be downloaded from here.

State of the Art Methods

The most relevant methods for large-scale global optimization are:

• Real-coded CHC (Eshelman, L.J., Schaffer, J.D. (1993). Real-coded genetic algorithms and interval-schemata. In: Foundations of Genetic Algorithms 2, L. D. Whitley, Ed. San Mateo, CA: Morgan Kaufmann, p. 187–202).
• G-CMA-ES (Auger, A., Hansen, N. (2005). A restart CMA evolution strategy with increasing population size. In: Proc. of the 2005 IEEE Congress on Evolutionary Computation, p. 1769-1776).
• Differential Evolution (DE) (Storn, R., Price, K. (1997). Differential evolution – a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization 11 (4), 341–359).
• Scatter Tabu Search (STS) (Duarte, A., Martí, R., Glover, F., Gortázar, F. (2010). Hybrid scatter tabu search for unconstrained global optimization. Annals of Operations Research).

Computational Experience

All the experiments were conducted on a Pentium 4 computer at 3 GHz with 6 GB of RAM. The requirements on the simulation procedure are the following:

1. Each algorithm is run 25 times for each test function.
2. The performance measures that should be provided are:
• Average of error of the best individuals found in the 25 runs. For a solution x, the error measure is defined as: f(x)-f(op), where op is the optimum of the function.
• Maximum error achieved in the 25 runs.
• Minimum error achieved in the 25 runs.
• Median of the error achieved in the 25 runs.
3. The study should be made with dimensions D = 50, D = 100, D=200, D=500, and D = 1,000. The maximum number of fitness evaluations is 5,000·D. Each run stops when the maximal number of evaluations is achieved.

Results can be downloaded in Excel

References (Best Methods)

• Eshelman, L. J. and Schaffer, J. D. (1993) "Real-coded genetic algorithms and interval-schemata", Foundation of Genetic Algorithms 2, Morgan Kaufmann, 187--202.
• Auger, A., Hansen, N. (2005) "A restart CMA evolution strategy with increasing population size", Congress on Evolutionary Computation 2005, 1769-1776.
• Storn, R. and Price, K. (1997) "Differential Evolution -- A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces", Journal of Global Optimization, 11, 4, 341--359. doi:10.1023/A:1008202821328.
• Duarte, A., Martí, R., Glover, F., Gortázar, F. (2009) "Hybrid scatter tabu search for unconstrained global optimization", Annals of Operations Research. doi:10.1007/s10479-009-0596-2
• Duarte, A., Martí, F., Gortázar, F. (2010) "Path relinking for large-scale global optimization", Soft Computing - A Fusion of Foundations, Methodologies and Applications. doi:10.1007/s00500-010-0650-7