Problem Description

The capacitated single assignment hub location problem with modular link capacities is a variant of the classical hub location problem in which the cost of using edges is not linear but stepwise, and the hubs are restricted in terms of transit capacity rather than in the incoming traffic. This problem was introduced by Yaman and Carello (Yaman and Carello, 2005) and treated by a branch-and-cut and a tabu search metaheuristic. We propose a metaheuristic algorithm based on strategic oscillation, a methodology originally introduced in the context of tabu search. Our method incorporates several designs for constructive and destructive algorithms, together with associated local search procedures, to balance diversification and intensification for an efficient search. Computational results on a large set of instances show that, in contrast to exact methods that can only solve small instances optimally, our metaheuristic is able to find high-quality solutions on larger instances in short computing times. In addition, the new method, which joins tabu search strategies with strategic oscillation, outperforms the previous tabu search implementation.

In mathematical terms, given a network G with a set of nodes V and a set of edges E, let t_ij be the amount of traffic to be transported from node i to node j, where t_ij=0 for any node i.

Each node i is either a terminal node or a hub node (terminal and hub for short). A terminal can only be assigned to a single hub. A hub is assigned to itself. The hubs and the adges among them define a complete subgraph. Opening a hub at node i has a fixed installation cost of C_ii. Each hub i has a capacity Q^h limiting the total amount of traffic transitiing through i.

There are two types of edges between nodes: edges of the first type are used to connect terminals with hubs, and we call them access edges. Let m_i be the number of access edges needed to route the incoming and outgoing traffic at node i. The cost of installing m_i edges between terminal i and hub k is denoted by C_ik. Edges of the second type are used to transfer traffics between hubs, and we call them backbone edges. Each backbone edge has a maximum traffic capacity of Q^b (in each direction). If nodes k and l are hubs, the amount of traffic on arc (k,l), denoted as z_kl, is the traffic that has to be transported from nodes assigned to k to nodes assigned to l. The capacity Q^b of a given edge kl cannot be less than the maximum traffic on its corresponding arcs (k, l) and (l, k), and the cost of installing te edge is denoted by R_kl.

The following variables (Yaman and Carello, 2005) are defined in order to provide the mathematical programming model shown below: The assignment variable x_ik is equal to 1 if terminal i is assigned to hub k, and 0 otherwise. If node i receives a hub, then x_ii takes value 1. z_kl is the traffic on an arc (k,l) and w_kl is the number of copies of the edge kl.

The problem is formulated (Yaman and Carello, 2005) as:

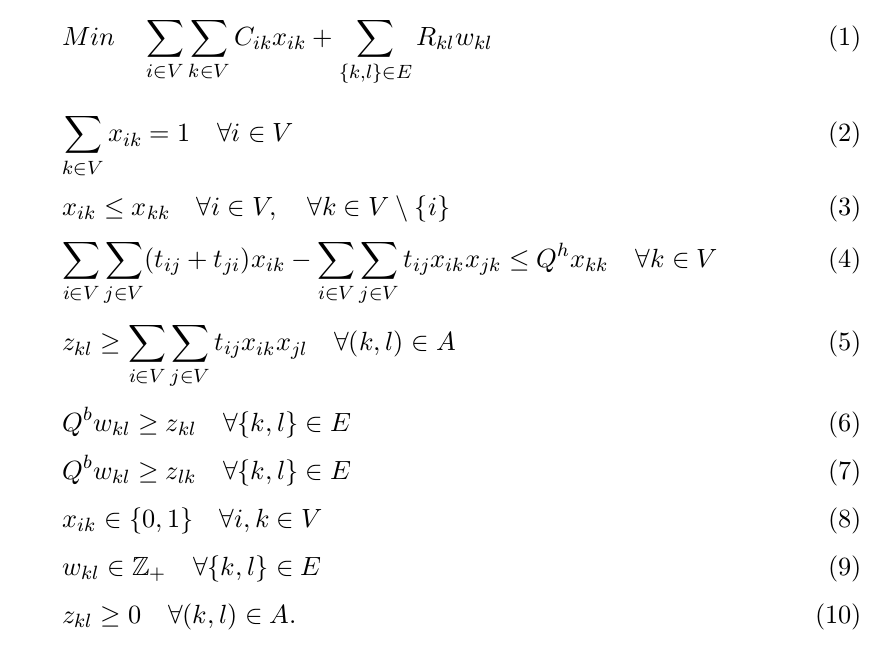
State of the Art Methods

A metaheursitic and a branch-and-cut algorithm were proposed in (Yaman and Carello, 2005). The metaheuristic consists of a tabu search (TS) to solve the hub location subproblem and a local search for assigning terminals to hubs. The solution provided by the metaheuristic is used as an initial upper bound in the branch-and-cut algorithm and to limit the number of variables considered by the exact method. In addition to the best solution, the metaheuristic produces also a subset of nodes that represents, in a sense, the best potential locations for the hubs. The hubs selected in the best solution belong to this subset, as well as the two other hubs which appear most often in the best solutions found by the metaheuristic. This set is called the concentration set. The resulting reduced problem, where hubs can be chosen only among the nodes of the concentration set, is called the concentrated problem, and is the problem solved using the branch-and-cut method.

A strategic oscillation algorithm that incorporates several designs for constructive and destructive phases, making use of tabu search memory structures together with associated local search procedures.

Instances

We have tested our algorithms on three sets of instances:

1. The CAB (Civil Aviation Board) data set. It is based on airline passenger flows between some important cities in the United States. It consists of a data file, presented by O’Kelly in 1987, with the distances and flows of a 25 nodes graph.
2. The AP (Australian Post) data set. It is based on real data from the Australian postal service and was presented by Ernst and Krishnamoorthy in 1996. The size of the original data file is 200 nodes. Smaller instances can be obtained using a code from ORLIB. As with CAB, many authors have generated different instances from the original file.
3. The USA423 data set. Introduced by (Peiró, Corberán, and Martí, 2014) and based on real airline data. It consists of a data file concerning 423 cities in the United States, where real distances and passenger flows for an accumulated 3 months period are considered.

You can download the instances here.

Computational Experience

We performed extensive computational experiments with 150 instances. The best values for the instances can be downloaded here.