Vertex Bisection Problem
Herrán A., Colmenar J. M., Duarte A. (2018)
Optsicom project, University of Valencia (Spain)
Problem Description
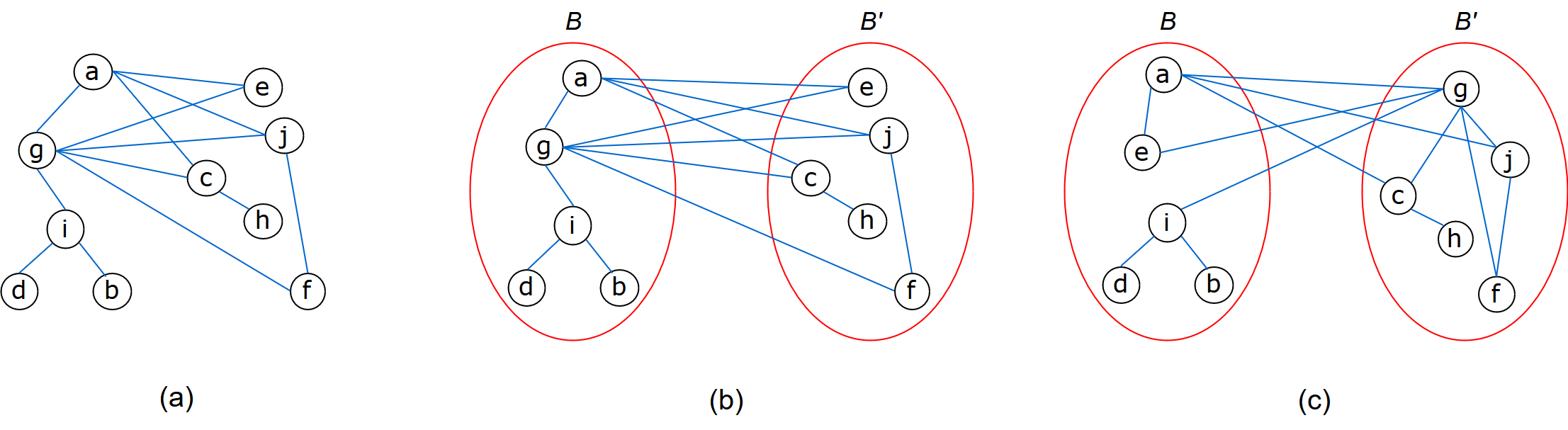
The Vertex Bisection Problem (VBP) belongs to the family of well-known graph partitioning problems, where the main goal is to find a partition of the vertices maximizing or minimizing a given objective function. In particular, VBP consists of dividing a graph into two parts B and B’ with the same number of vertices, or differing in one if the number of vertices is odd, such as the vertex width (VW), defined as the number of vertices in B with at least one adjacent in B’, is minimized. As example, Figure (a) shows a connected undirected graph with 10 vertices and 13 edges. Figures (b) and (c) show two feasible solutions for the VBP with a vertex width of 2 and 3 respectively.
More formally, given a graph G = (V,E) where V is the set of vertices, |V| = n, and E is the set of edges, a feasible solution of the VBP is defined by two subsets of nodes B and B’ (with B ∩ B’ = ∅ and B ∪ B’ = V) where the size of each subset verifies that B = ⌊n/2⌋ and B’ = n – ⌊n/2⌋, respectively. Hence, given a solution S = (B, B’), its vertex width is computed as:
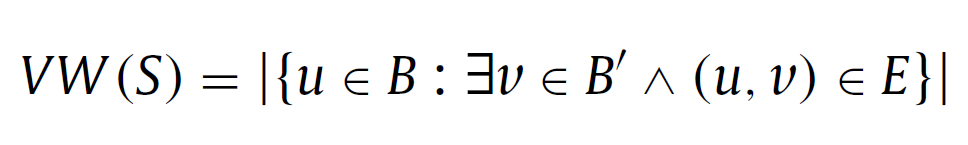
Let 𝒮 be the whole set of feasible partitions of V according to the aforementioned constraints. Therefore, the VBP consists of finding the solution S* ∈ 𝒮 that minimizes the vertex width.
State of the Art Methods
This problem has been dealt with from both, exact and heuristic perspectives. Among the exact methods, the most relevant works are:
- B&B: Branch & Bound algorithm for the two proposed integer-linear programming models. Fraire (2014).
- QCQP: Quadratically constrained quadratic program for a different integer-linear programming model than the proposed in (Fraire, 2014). Jain (2016a).
- B&B: Branch & Bound algorithm that incorporates a greedy heuristic to produce an upper bound for the cost of the solutions. Jain (2016b).
The most relevant heuristic methods developed to solve this problem are:
- CH: Different constructive heuristics. Castillo-Garcia (2015).
- GA: Genetic algorithm. Huacuja (2016).
- MA: Memetic algorithm. Pallavi (2016).
Instances
Our experimental experience is developed on several sets of instances with different number of vertices, edges, and densities. These sets contain Small-Full (84), Trees (15), Grids (5) and HB (4) instances used in Fraire (2014), and the Small (23), Harwell-Boeing (36) and Hypercubes (8) instances used in (Pallavi, 2016).
We stored the resulting 175 instances as a library that we called VBP_LIB:
Computational Experience
All the algorithms were implemented in C++ and the experiments were conducted on an Intel i7 6500U processor running at 2.5 GHz with 8 Gb of RAM using Windows 10. We have considered the VBP_LIB instances described above. The individual results for each instance can be downloaded here in Excel format.
Vertex Bisection problem results
References
- H. Fraire, J. Terán-Villanueva, N.C. García, J. Gonzalez-Barbosa, E.R. del Angel, Y. Gómez-Rojas. Exact Methods for the Vertex Bisection Problem. Springer International Publishing (2014), pp. 567–577.
- P. Jain, G. Saran, K. Srivastava. A new integer linear programming and quadratically constrained quadratic programming formulation for vertex bisection minimization problem. J. Autom. Mobile Rob. Intell. Syst. 10(1) (2016a), pp. 69–73.
- P. Jain, G. Saran, K. Srivastava. Branch and bound algorithm for vertex bisection minimization problem. In: R.K. Choudhary, J.K. Mandal, N. Auluck, H.A. Nagarajaram (Eds.), Advanced Computing and Communication Technologies, Proceedings of the 9th ICACCT (2015), Springer Singapore, Singapore (2016b), pp. 17–23.
- N. Castillo-García, H.J.F. Huacuja, J.A.M. Flores, R.A.P. Rangel, J.J.G. Barbosa, J.M.C. Valadez. Comparative Study on Constructive Heuristics for the Vertex Separation Problem. Springer International Publishing, Cham (2015), pp. 465–474.
- H.J.F. Huacuja, N. Castillo-García. Optimization of the vertex separation problem with genetic algorithms. IGI Global (2016), pp. 13–31.
- J. Pallavi, G. Saran, K. Srivastava. On minimizing vertex bisection using a memetic algorithm. Inf. Sci. 369 (2016), pp. 765–787.