Uncapacitated r-Allocation p-Hub Median Problem
Peiró J., Corberán A., Martí R. (2013)
Optsicom project, University of Valencia (Spain)
Problem Description
The Uncapactitated r-Allocation p-Hub Median Problem (UrApHMP) is a variant of the classical p-hub problem. Hub location problems arise when given a set of nodes with pairwise traffic demands, we have to choose p of them as hub locations and route all the traffic through these hubs at a minimum cost. For each pair of nodes i and j, there is a traffic tij that needs to be transported. It is generally assumed that direct transportation between non-hub nodes is not possible, and the tij traffic travels on a path i→hi→hj→j, where hi and hj are hubs assigned to i and j, respectively.
Recently, Yaman (2011) proposed the UrApHMP, a very interesting variant of this classical location problem in which each node can be connected to at most r of the p hubs. The motivation of this variant comes from the fact that the single allocation version, in which a node is connected (assigned) to a single hub is too restricted for real-world situations, while the multiple allocation variant, where each node can use any of the p hubs to route its traffic, results in high fixed costs and complicated networks. The r-allocation p-hub problem, being r≤p, generalizes both versions of the p-hub median problem. When r=1we are at the single allocation version, whereas if r=p, we have the multiple allocation version.
In mathematical terms, given a network with a set of nodes N and a set of arcs A, let tij be the amount of traffic to be routed from node i to node j, i.e., through the arc (i,j), and let dij be its associated unit routing cost. The UrApHMP is then formulated (Yaman, 2011) in terms of the following variables: Given a node k, zkk=1 if the node is a hub (i.e., if a hub is set or located at this node), and zkk=0 otherwise. Given a non-hub node i and a hub k, zik=1 if node i is assigned or allocated to node k, and 0 otherwise. Finally, fijkl is the proportion of the traffic tij from node i to node j that travels along the path i→k→l→j, where k and l are hubs. With these variables, the problem can be formulated as follows:
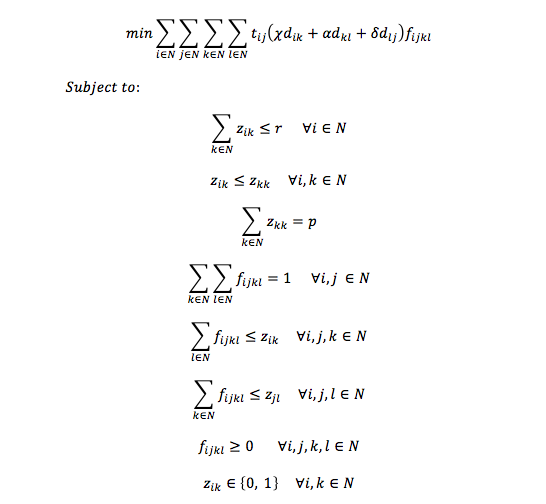
The p-hub median problem belongs to the class of NP-hard problems. Even when the set of hubs is given, the sub-problem of optimal allocation of non-hub nodes to hubs is also NP-hard (Love, Morris and Wesolowski, 1988).
State of the Art Methods
A GRASP in which we consider three local search procedures. We also implement a filtering mechanism to discard low-quality constructions to help saving running time for large instances.
A scatter search algorithm in which we consider seven diversification generation methods, and path-relinking as an extension of the classical combination method.
Instances
We have tested our algorithms on three sets of instances:
- The CAB (Civil Aviation Board) data set. It is based on airline passenger flows between some important cities in the United States. It consists of a data file, presented by O’Kelly in 1987, with the distances and flows of a 25 nodes graph. From this original file, 75 instances with 25 nodes and p= 1,…, 5, and r= 1,…, p have been generated by several authors. The following parameter values have been widely used: χ=1,δ=1, and α= 0.2, 0.4, 0.6, 0.8, and 1.
- The AP (Australian Post) data set. It is based on real data from the Australian postal service and was presented by Ernst and Krishnamoorthy in 1996. The size of the original data file is 200 nodes. Smaller instances can be obtained using a code from ORLIB. As with CAB, many authors have generated different instances from the original file. We have extended this set of instances by generating 360 instances with n= 40, 50, 70, 75, 80, 85, 90, 95, 100, 150 and 200 nodes. For those instances with 40≤n≤50, p ranges from 1 to 5. For those with 70≤n≤95, p ranges from 1 to 8, and for those with 100≤n≤200, p takes values between 1 and 20. In all these cases, r<∈{1,…,p}. According with previous articles, cost parameter values are χ=3, α=0.75 and δ=2. Regarding the flows between nodes, these instances do not have symmetric flows (i.e., for a given pair of nodes iand j,tij is not necessarily equal to tji). Moreover, flows from one node to itself can be positive (i.e., tiican be strictly positive for a given i).
- The USA423 data set. This is a new family of instances that we introduce here based on real airline data. It consists of a data file concerning 423 cities in the United States, where real distances and passenger flows for an accumulated 3 months period are considered. From the original data, 30 instances have been generated with p∈{3,4,5,6,7} and 2≤r≤p-1. For each combination of parameters p and r, two different values for χ,α,δ have been used: 0.1, 0.07, 0.09, and 0.09, 0.075, 0.08, respectively.
You can download the instances here.
Computational Experience
We performed extensive computational experiments with 465 instances. The best values for the hardest instances can be downloaded here.
References
- Aiex, R. M., M. G. C. Resende, and C. C. Ribeiro. 2007. TTT plots: A perl program to create time-to-target plots. Optimization Letters 1, no. 4: 355-366.
- Alumur, S., and Kara, B. Y. Network hub location problems: The state of the art. European Journal of Operational Research 190, 1 (2008), 1-21.
- Campbell, J. F. 1994. Integer programming formulations of discrete hub location problems. European Journal of Operational Research 72, no. 2: 387-405.
- Campbell, J. F. and M. E. O’Kelly. 2012. Twenty-five years of hub location research. Transportation Science 46, no. 2: 153-169.
- Contreras, I., and Fernández, E. General network design: A unified view of combined location and network design problems. European Journal of Operational Research 219, 3 (2012), 680-697.
- Correia, I., Nickel, S., and Saldanha da Gama, F. Hub and spoke network design with single-assignment, capacity decisions and balancing requirements. Applied Mathematical Modelling 35, 10 (2011), 4841-4851.
- Díaz, J. A., and Fernández, E. Hybrid scatter search and path relinking for the capacitated p-median problem. European Journal of Operational Research 169, 2 (2006), 570-585.
- Ernst, A. and M. Krishnamoorthy. 1996. Efficient algorithms for the uncapacitated single allocation p-hub median problem. Location Science 4, no. 3: 139-154.
- Farahani, R. Z., Hekmatfar, M., Arabani, A. B., and Nikbakhsh, E. Hub location problems: A review of models, classification, solution techniques, and applications. Computers & Industrial Engineering 64, 4 (2013), 1096-1109.
- Feo, T. A. and M. G. C. Resende. 1989. A probabilistic heuristic for a computationally difficult set covering problem. Operations Research Letters 8, no. 2: 67-71.
- Feo, T. A. and M. G. C. Resende. 1995. Greedy randomized adaptive search procedures. Journal of Global Optimization 6, no. 2: 109-133.
- Festa, P. and M. G. C. Resende. 2011. GRASP: Basic components and enhancements. Telecommunication Systems 46, no. 3: 253-271.
- García, S., M. Landete, and A. Marín. 2012. New formulation and a branch-and-cut algorithm for the multiple allocation p-hub median problem. European Journal of Operational Research 220, no. 1: 48-57.
- Gelareh, S. and S. Nickel. 2011. Hub location problems in transportation networks. Transportation Research Part E: Logistics and Transportation Review 47, no. 6: 1092-1111.
- Glover, F. A template for scatter search and path relinking. In Artificial Evolution, J.-K. Hao, E. Lutton, E. Ronald, M. Schoenauer, and D. Snyers, Eds., Lecture Notes in Computer Science 1363, Springer (1998), pp. 13-54.
- Glover, F. Tabu search and adaptive memory programing – advances, applications and challenges. In Interfaces in Computer Science and Operations Research (1996), Kluwer, pp. 1-75.
- Glover, F., Laguna, M., and Martí, R. Fundamentals of scatter search and path relinking. Control and Cybernetics 29, 3 (2000), 652-684.
- Ilić, A., D. Urosević, J. Brimberg, and N. Mladenović. 2010. A general variable neighborhood search for solving the uncapacitated single allocation p-hub median problem. European Journal of Operational Research 206, no. 2: 289-300.
- Kratica, J., Z. Stanimirović, D. Tosić, and V. Filipović. 2007. Two genetic algorithms for solving the uncapacitated single allocation p-hub median problem. European Journal of Operational Research 182, no. 1: 15-28.
- Labbé M., and Yaman, H. Solving the hub location problem in a star-star network. Networks 51, 1 (2008), 19-33.
- Laguna, M. and R. Martí. 1999. GRASP and path relinking for 2-layer straight line crossing minimization. INFORMS Journal on Computing 11, no. 1: 44-52.
- Laguna, M., and Martí, R. Scatter Search: Methodology and Implementations in C. Kluwer Academic Publishers (2002).
- Love, R.F., Morris, J.G., and Wesolowski, G.O. 1988. Facilities location: Models and methods. Elsevier Science Publishing Co., New York.
- Martí, R., Laguna, M., and Glover, F. Principles of scatter search. European Journal of Operational Research 169, 2 (2006), 359-372.
- Milanović, M. 2010. A new evolutionary based approach for solving the uncapacitated multiple allocation p-hub median problem. In Soft Computing in Industrial Applications, AISC 75 (X. Z. Gao et al., eds.). Springer-Verlag, Berlin, pp: 81-88.
- O’Kelly, M. E. 1987. A quadratic integer program for the location of interacting hub facilities. European Journal of Operational Research 32, no. 3: 393-404.
- Pacheco, J. A., and Casado, S. Solving two location models with few facilities by using a hybrid heuristic: A real health resources case. Computers & Operations Research 32, 12 (2005), 3075-3091.
- Resende, M. G. C., Ribeiro, C. C., Glover, F., and Martí, R. Scatter search and path-relinking: Fundamentals, advances, and applications. In Handbook of Metaheuristics, M. Gendreau and J. Y. Potvin, Eds., International Series in Operations Research & Management Science 146. Springer (2010), pp. 87-107.
- Resende, M. G. C., and Werneck, R. F. A hybrid heuristic for the p-median problem. Journal of Heuristics 10, 1 (2004), 59-88.
- Ribeiro, C. C., and Resende, M. G. C. Path-relinking intensification methods for stochastic local search algorithms. Journal of Heuristics 18, 2 (2012), 193-214.
- Yaman, H. 2011. Allocation strategies in hub networks. European Journal of Operational Research 211, no. 3: 442-451.