Obnoxious p-Median Problem
Colmenar, J. M., Greistorfer, P., Martí, R., Duarte A. (2016)
Optsicom project, University of Valencia (Spain)
Problem Description
Let I be a set of clients, J a set of facilities, and dij the distance between the client i ∈ I and the facility j∈ J. The Obnoxious p-Median (OpM) problem consists in finding a set S with p facilities (with S ⊆ J and p< |J|), such that the sum of the minimum distance between each client and the set of facilities is maximized. In mathematical terms:
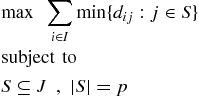
State of the Art Methods
The OpM problem was introduced in the 1990s (Cappanera, 1999, Eiselt, Laporte, 1995 and Welch, Salhi, 1997) and, as of today, has only gained relatively few attention. It is NP-hard (Tamir, 1991) and can be formulated as a binary LP. Note that Burkard, Fathali, and Taghizadeh Kakhki (2007) proved that the special case of the OpM problem on a tree can be solved in linear time. A branch and cut method coupled with a tabu search has been recently suggested by Belotti, Labbé, Maffioli, and Ndiaye (2007).
Instances
We have used a set of 144 instances in our experimentation. In particular, they were generated by considering 24 instances of the well-known p-median problem. To this aim we considered the instances from pmed17 to pmed40, where the number of nodes ranges from 400 to 900. These p-median instances are found in the OR-Library (Beasley, J. J Oper Res Soc (1990) 41: 1069. doi:10.1057/jors.1990.166).
In order to transform a p-median instance into an obnoxious p-median one, Belotti et al. (2007) described the following procedure. Given the original instance with n nodes, this method selects n/2 nodes at random to be the set of clients. The remaining n/2 become the set of facilities. Additionally, for each original instance, Belotti et al. (2007) derived three new instances for the OpM by considering three values of p: ⌊n/2⌋, ⌊n/4⌋ and ⌊n/8⌋.
We folowed that process to generate the instances and then, for each one of the resulting files, we generated an A and a B version of them by transposing the table that stores the distances between clients and facilities. This is a simple way of obtaining two different instances with similar charasteristics for each one of the processed files.
Hence, we stored the resulting 144 instances as a library that we called OpM_LIB:
Computational Experience
All the algorithms were implemented in Java SE 7 and the experiments were conducted on an Intel Core i5 660 CPU (3.3 GHz) and 8 GB RAM. We have considered the OpM_LIB instances described above. The individual results for each instance can be downloaded here in Excel format.
Obnoxious p-Median problem results
References
- J. E. Beasley. OR-Library: Distributing test problems by electronic mail. Journal of the Operational Research Society, 41 (11) (1990), pp. 1069–1072.
- P. Belotti, M. Labbé, F. Maffioli, M. Ndiaye. A branch-and-cut method for the obnoxious p-median problem.4OR, 5 (4) (2007), pp. 299–314.
- R. Burkard, J. Fathali, H. Taghizadeh Kakhki. The p-maxian problem on a tree. Operations Research Letters, 35 (3) (2007), pp. 331–335.
- P. Cappanera. A Survey on obnoxious facility location problems. Technical report Dipartimento di Informatica, Università di Pisa (1999).
- H. Eiselt, G. Laporte. Objectives in location problems. Z. Drezner (Ed.), Facility location. a survey of applications and methods., Springer, New York (1995), pp. 151–180.
- A. Tamir. Obnoxious facility location on graphs. SIAM Journal on Discrete Mathematics, 2 (4) (1991), pp. 550–567.
- S. Welch, S. Salhi. The obnoxious P facility network location problem with facility interaction. European Journal of Operational Research, 102 (1997), pp. 302–319.