Equitable Dispersion Problem
Martí R., Sandoya F. (2012)
University of Valencia (Spain), Escuela Superior Politécnica del Litoral (Ecuador)
Problem Description
The Equitable Dispersion Problem (EDP) consists in selecting a subset of elements, whose cardinality is not fixed in advance, from a given set in such a way that maximizes the equity among elements. There are several equity measures in the framework of the EDP. These equity measures may also arise in the contexts ofdiverse/similar group selection,identifying diverse groups of people, and diversificationor assimilation among members of a network.
In particular, we target the Max-Mean dispersion model in which the average distance between the selected elements is maximized, this measure is used to balance the dispersion among individual elements. This model is especially suited for instances in which the distances represent affinity and are not restricted to take non-negative values.
In mathematical terms, given a set N of n elements and dij the affinity between any elements i and j, the Max-Mean DP consists of selecting a subset M of N in such a way that the dispersion mean dm(M), in terms of the affinity values, is maximized.
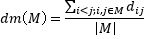
The dm(M) value reflects an equity measure based on an average dispersion. The Max-Mean Dispersion Problem can be trivially formulated with binary variables as:
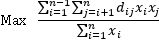
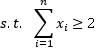
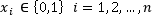
Where variable xi takes the value 1 if element i is selected and 0 otherwise. Note that the number of selected elements, |M|, is not set a priori as in the rest of diversity models, such as the MDP or the MMDP, where it is pre-specified as a problem constraint.
Prokopyev (2009) showed that the Max-Mean dispersion problem is strongly NP-hard if the distances (diversity measure) take both positive and negative values.
State of the Art Methods
The metaheuristics developed to solve the Max-Mean dispersion problem are:
- GRASP1: GRASP based heuristic developed as a modified version of heuristic1 proposed by Prokopyev (2009)for solving Max-Minsum DP, which is a somewhat similar problem. Martí and Sandoya (2012)
- GRASP2: GRASP based method developed as a modified version of GRASP_C2, proposed by Duarte and Martí (2007) for the Max-Sum model. Martí and Sandoya (2012)
- GRASP3+PR: Hybrid method that combines GRASP methodology with a Variable Neighborhood Search improvement method and Path-Relinking. Martí and Sandoya (2012)
- TS: Tabu Search with dynamic tenure and a diversification stage. Carrasco et al. 2014.
Instances
Most of the previous works on diversity limit themselves to problems with non-negative distances. However, as described in Glover et al. (1998), the diversity measure can be something in the nature of an affinity relationship, which expresses a relative degree of attraction between the elements as arises in settings with a behavioral component. We have constructed two sets of instances where, as explained above, the distances can take both negative and positive values.
- Type I: This data set consists of 60 symmetric matrices with random numbers between -10 and 10 generated from a uniform distribution. They can represent the affinity between individuals in a social network. We generate 10 instances for each size of n = 20, 25, 30, 35, 150, 500, 750, and 1000.
- Type II: This data set consists of 60 symmetric matrices with random numbers in [-10,-5] U [5,10]. These instances can reflect the polarization that occurs when people get together in groups. We can identify clusters of individuals with a high attraction within clusters and a high repulsion between clusters and with no room for indifference. We generate 10 instances for each size of n= 20, 25, 30, 35, 150, 500, 750, and 1000.
You can download the instances here.
Computational Experience
We performed extensive computational experiments, with 160 instances, the final optimum values or best values for the instances can be downloaded here.
References
Carrasco, R., Anthanh P. T., Gallego M., Gortázar F., Duarte A., Martí R. “Tabu Search for the Max-Mean Dispersion Problem“. Submitted to Knowledge Based Systems.
Martí R., Sandoya F. “GRASP and Path Relinking for the Equitable Dispersion Problem”. Computers & Operations Research, 2012.To appear
Prokopyev O.A., Kong N, Martinez-Torres DL. ”The equitable dispersion problem”, European Journal of Operational Research, 197: 59-67, (2009)
Duarte A, Martí R. “Tabu Search and GRASP for the Maximum Diversity Problem”, European Journal of Operational Research; 178, 71-84, (2007)
Page, S.E. (2007), The difference – How the power of diversity creates better groups, firms, schools, and societies, Princeton University Press.
Resende, M.G.C. and Ribeiro, C.C. “Greedy Randomized Adaptive Search Procedures”, State of-the-art Handbook in Metaheuristics, F. Glover and G. Kochenberger (Eds.), Kluwer Academic Publishers, Boston, pp. 219-250, (2001)
Glover, F., Kuo, C.C. and Dhir K.S., ”Heuristic Algorithms for the Maximum Diversity Problem”, Journal of Information and Optimization Sciences, vol. 19 (1), 109-132, (1998)