Biorienteering Problem
Martí, Campos, Resende and Duarte (2012)
University of Valencia (Spain), AT&T Labs (USA) and University Rey Juan Carlos (Spain)
Problem Description
The bi-orienteering problem (BOP) considered here is a bi-objective optimization problem that is a generalization of the single-objective version also known as the selective traveling salesman problem, introduced by Tsiligirides (1984). In the orienteering problem, each vertex of a given directed graph G=(V, A) has two different profits. The aim of this problem is to select a subset of vertices in order to maximize the sum of both profits. Moreover, the tour visiting the selected vertices cannot exceed a maximum length (or time). The motivation of this problem was the planning of a set of tourist routes in a large city. Each point of interest has different profits associated with different activities (say for instance culture and leisure). Since the maximization of the profits associated with one activity does not imply the maximization of the profits of another activity, this problem is multi-objective in nature.
There are several problems related with the orienteering problem. For instance, in the Prize-Collecting TSP, see Balas (1988), each vertex has a given prize and penalty, and the goal is to minimize the length of the tour plus the total of the penalties of the vertices not in the tour, while collecting a given quota of the prizes. Feillet, Dejax and Gendreau (2005) classified these problem types as TSP with profits. Archetti, Hertz and Speranza (2007) extended the TSP with profits to several tours naming this version the Vehicle Routing Problem (VRP) with profits. Note that all of them are mono-objective approaches to similar problems. Recently however, Schilde, Doerner, Hartl and Kiechle (2009) proposed two metaheuristic procedures for solving the bi-objective orienteering problem. The first is based on Ant Colony Optimization (ACO), introduced by . Dorigo and Gambardella (1997) and the second is based on Variable Neighborhood Search (VNS). See the seminal paper by Mladenovic and Hansen (1997). Both algorithms were combined with a Path Relinking procedure. A detailed formulation of the general form of BOP when considering multi-objective functions can be found in Schilde, Doerner, Hartl and Kiechle (2009).
The bi-objective OP, called BOP, can be stated on a directed graph G=(V,A) with V = {0, 1, 2, ..., n + 1} the set of vertices and A ={(i, j) : i, j in V, i ≠ j, i ≠ n + 1, j ≠ 0} the set of arcs. Without loss of generality we suppose that G is a complete graph with associated cost cij for (i, j) in A. We have two profits fi1, fi2 associated with each vertex i in V \ {0, n + 1}. Both vertices 0 and n + 1 have no profits and represent the starting and ending vertices, respectively. Sometimes vertices 0 and n + 1 denote the same physical point. A tour in the original problem is represented by a directed path in G from vertex 0 to vertex n + 1. Let L be the maximum length allowed to tour τ and consider the set of all feasible tours Θ = {τ : c(τ) ≤ L}.
With these elements the BOP can be formulated as:
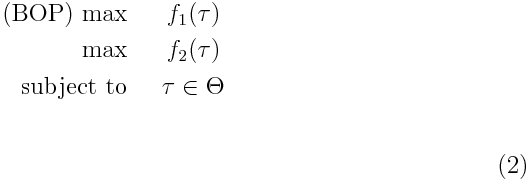
State of the Art Methods
The most relevant procedures developed to solve this problem are:
- ACO: Ant Colony Optimization. Schilde et al (2009)
- VNS: Variable Neighborhood Search. Schilde et al (2009)
- GRASP+PR: Multiobjective GRASP with Path Relinking. Martí et al (2012)
Instances (BOP)
We have compiled a comprehensive set of benchmark problems including all problem instances which have so far been used for conducting computational experiments for the BOP. Specifically, previous method reports results over a set of 10 BOP test instances with vertices ranging from 21 to 2143 (see Schilde et al, 2009). These authors collected them from different sources. Specifically, they are: 2-p21, 2-p32, 2-p33, 2-p64, 2-p66, 2-p97, 2-p292, 2-p559, 2-p562, and 2-p2143. Additionally, we have generated 10 medium sized instances to calibrate the methods. The resulting instances are available here
Computational Experience
We have performed an intensive experimentation with the best know methods (run for the same CPU time) to compute an approximation of the efficient set for the instances. The final results for the instances can be downloaded here.
References
- T. Tsiligirides (1984) Heuristic methods applied to orienteerin. Journal of the Operational Research Society, 35(9): 797--809.
- E. Balas (1988) The prize collecting traveling salesman problem. Networks, 19(6):621--636.
- D. Feillet, P. Dejax and M. Gendreau (2005) Traveling salesman problems with profits. Transportation Science, 39(2):188--205.
- C. Archetti, A. Hertz and M.G. Speranza (2007) Metaheuristics for the team orienteering problem. Journal of Heuristics, 13(1):49--76.
- M. Schilde, K.F.Doerner, R.F.Hartl and G.Kiechle (2009) Metaheuristics for the bi-objective orienteering problem. Swarm Intelligence, 3:179--201.
- M. Dorigo and L.M. Gambardella (1997) Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Transactions on Evolutionary Computation, 1(1):53--66.
- M. Mladenovic and P. Hansen (1997) Variable neighborhood search. Computers and Operations Research, 24(11):1097--1100.
- Martí R, Campos, V, Resende, MGC, Duarte A.: Multiobjective GRASP with Path Relinking. Technical Report, 2012.